

The relative machine precision usually the smallest positive number such that fl( 1.0 - eps ) < 1.0, where fl denotes the computed value and eps is the relative machine precision. If this quantity is much larger than 1, the solution is probably incorrect. The Norm Res should be about O(1) in size. The test is based on || Ax - b || / ( || A || || x || eps) where eps is described below. The time in seconds to solve the problem, Ax=b.Ī check is made to show that the computed solution is correct. For this problem there are 2/3 n^3 + n^2 floating point operations. A floating point operation here is a floating point addition or a floating point multiplication with 64 bit operands.
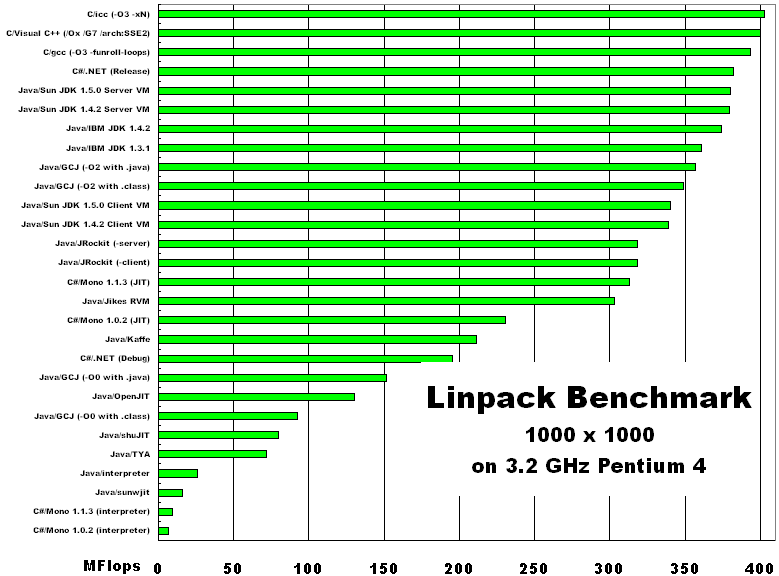
Millions of floating point operations per second. The result is reported in millions of floating point operations per second (MFLOP/s, sometimes simply called FLOPS). The solution is obtained by Gaussian elimination with partial pivoting, with 2/3 Introduced by Jack Dongarra, they measure how fast a computer solves a dense N by N system of linear equations Ax = b, which is a common task in engineering. The LINPACK Benchmarks are a measure of a system's floating point computing power. 826668 e - 02 pass Performance Summary ( GFlops ) Size LDA Align. Time ( s ) GFlops Residual Residual ( norm ) Check 1000 1000 4 0. Current date / time : Wed Feb 12 12 : 10 : 47 2020 CPU frequency : 4. xlinpack_xeon64 - i lininput_xeon64 Sample data file lininput_xeon64.


 0 kommentar(er)
0 kommentar(er)
